Skip to main content

Gauss's central difference formula for equal intervals.

 Gauss's central difference formula for equal intervals:

We shall develop central difference formulae which are best suitable for interpolation near the middle of the tabulated set (table).
x:             x₋₂  x₋₁  x₀  x₁  x₂
y=f(x):    y₋₂  y₋₁  y₀  y₁  y₂
Difference table
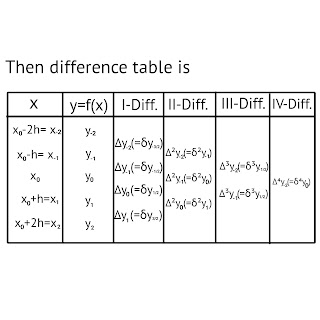Difference table.


Gauss's forward interpolation formula for equal intervals:

f(x) = y₀+[u/1!]∆y₀+{[u(u-1)]/2!}∆²y₋₁+{[(u+1)(u)(u-1)]/3!}∆³y₋₁+{[(u+1)u(u-1)(u-2)]/4!}∆⁴y₋₂ +......., Where u= (x-x₀)/h
Remark:
This formula is applicable when u lies between 0 and 1 i.e (0<u<1).
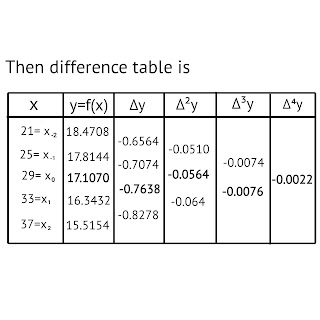
Example: Using Gauss's forward formula to evaluate y₃₀ given that y₂₁=18.4708, y₂₅=17.8144, y₂₉=17.1070, y₃₃=16.3432 and y₃₇=15.5154.
Solution. The difference table is
Forward difference table
Forward difference table.

To find y=f(x) at x=30, i.e f(30):
Taking x₀ = 29, h=4, x=30, then u= (x-x₀)/h = (30-29)/4 = 0.25
Using Gauss's forward difference formula
f(x) = y₀+[u/1!]∆y₀+{[u(u-1)]/2!}∆²y₋₁+{[(u+1)(u)(u-1)]/3!}∆³y₋₁+[(u+1)u(u-1)(u-2)/4!]∆⁴y₋₂ +......
=> f(30) = y₃₀ = 17.1070+(0.25)(-0.7638) + [(0.25)(-0.75)]/2×(-0.564) + [(1.25)(.25)(-.75)]/6×(-0.0076) + [(1.25)(.25)(-0.75)(-1.75)]/24× (-0.0022)
=> f(30) = y₃₀ = 17.1070-0.19095+0.00529+0.0003-0.00004
=>  y₃₀ = 16.92 Ans.

Gauss's backward interpolation formula:

f(x) = y₀+[u/1!]∆y₋₁+{[u(u+1)]/2!}∆²y₋₁+{[(u+1)(u)(u-1)]/3!}∆³y₋₂+[(u+2)(u+1)u(u-1)/4!]∆⁴y₋₂ +......., Where u= (x-x₀)/h
Remark:
This formula is applicable when u lies between -1 and 0.
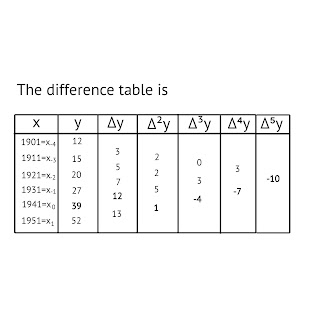
Example: Find by Gauss's backward formula the sales of a concern for the year 1936, given that
Year:                                                1901   1911   1921    1931   1941   1951
Sale( in thousands rupees):        12       15   20         27         39         52
Solution. Taking the origin at 1941 and h=10,
u= (x-x₀)/h= (1936-1941)/10 = -0.5.   [∵-1<u<0]
The central table is:
Forward difference table
Forward difference table.

Using Gauss backward formula:
f(x) = y₀+[u/1!]∆y₋₁+{[u(u+1)]/2!}∆²y₋₁+{[(u+1)(u)(u-1)]/3!}∆³y₋₂+.......
=> f(1936)= 39 + (-.5)×(12)+[(.5)(-.5)]/2 × [(.5)(-.5)(-1.5)]/6 ×(-4)
=> f(1936)= 39-6-0.125-0.25 = 32.625 thousands Ans.

Comments

Post a Comment

Popular posts from this blog

Different operators

 Different operators We will study the following operators: 1) The Shifting Operator (E): Ef(x) = f(x+h) i.e Ey₀= y₁ E²f(x) = f(x+2h) i.e E²y₀ = y₂ Eⁿf(x) = f(x+nh) i.e Eⁿy₀ = yₙ Here n takes integral or fractional, positive or negative values. For example: E⁻¹f(x) = f(x-h) i.e E⁻¹ y₂ = y₁ E¹/²f(x) = f[x+(1/2)h] i.e E¹/² y₁ = y₃ₗ₂ Properties of Operator E 1) Operator E is distributive. 2) Operator E is commutative with respect to constant. 3) Operator E obeys laws of indices. 2) Forward difference operator (∆): If x₀, x₁,x₂,......., xₙ are equally spaced with interval of differencing h and if y = f(x), then  ∆f(x) = f(x+h) - f(x) i.e ∆yᵢ = yᵢ₊₁ - yᵢ for i = 0,1,2,3,..... n-1, The symbol ∆ is called forward difference operator and  ∆yᵢ is called first forward difference. Similarly, the second forward differences are ∆²yᵢ =∆yᵢ₊₁ - ∆yᵢ For example: ∆²y₀ =∆y₁ - ∆y₀ = (y₂ - y₁)-(y₁-y₀)                           ...
Post a Comment
Read more

Questions (Forward difference operator, Backward difference operator and Shifting operator)

Questions Example: Given that y₅=4, y₆=3, y₇=4, y₈=10, y₉=24, find the value of ∆⁴y₅: (i) By using the difference table and (ii) Without using the difference table. Solution: (i) Forward difference table. From the difference table ∆⁴y₅=0. Ans. (ii) We have ∆⁴y₅= (E-1)⁴y₅ [∵ ∆=E-1]                               = (E⁴-4E³+6E²-4E+1)y₅                               = E⁴y₅-4E³y₅+6E²y₅-4Ey₅+1y₅                               = y₉ -4y₈+6y₇-4y₆+y₅ [Eⁿyₓ=yₓ₊ₙ]                               = 24-4×10+6×4-4×3+4                               = 24-40-24-12+4 =0Ans. Example: Given x:  1     2     3...
Post a Comment
Read more